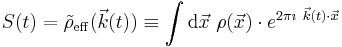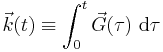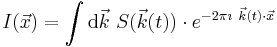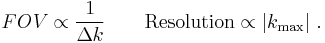Physics of magnetic resonance imaging
- This is a sub-article to Magnetic resonance imaging
The body is largely composed of water molecules which each contain two hydrogen nuclei or protons. When a person goes inside the powerful magnetic field of the scanner, the magnetic moments of these protons align with the direction of the field.
A radio frequency electromagnetic field is then briefly turned on, causing the protons to alter their magnetization alignment relative to the field. When this field is turned off the protons return to the original magnetization alignment. These magnetization alignment changes create a signal which can be detected by the scanner. The frequency at which the protons resonate depends on the strength of the magnetic field. The position of protons in the body can be determined by applying additional magnetic fields during the scan which allows an image of the body to be built up. These are created by turning gradient coils on and off which creates the knocking sounds heard during an MRI scan.
Diseased tissue, such as tumors, can be detected because the protons in different tissues return to their equilibrium state at different rates. By changing the parameters on the scanner this effect is used to create contrast between different types of body tissue.
Contrast agents may be injected intravenously to enhance the appearance of blood vessels, tumors or inflammation. Contrast agents may also be directly injected into a joint in the case of arthrograms, MRI images of joints. Unlike CT, MRI uses no ionizing radiation and is generally a very safe procedure. Patients with some metal implants, cochlear implants, and cardiac pacemakers are prevented from having an MRI scan due to effects of the strong magnetic field and powerful radio frequency pulses.
MRI is used to image every part of the body, and is particularly useful for neurological conditions, for disorders of the muscles and joints, for evaluating tumors, and for showing abnormalities in the heart and blood vessels.
Contents |
Nuclear magnetism
Subatomic particles have the quantum mechanical property of spin.[1] Certain nuclei such as 1H (protons), 2H, 3He, 23Na or 31P, have a non–zero spin and therefore a magnetic moment. In the case of the so-called spin-1⁄2 nuclei, such as 1H, there are two spin states, sometimes referred to as "up" and "down". Nuclei such as 12C have no unpaired neutrons or protons, and no net spin; however, the isotope 13C does.
When these spins are placed in a strong external magnetic field they precess around an axis along the direction of the field. Protons align in two energy "eigenstates" (the "Zeeman effect"): one low-energy and one high-energy, which are separated by a very small splitting energy.
Resonance and relaxation
In the static magnetic fields commonly used in MRI, the energy difference between the nuclear spin states corresponds to a radio frequency photon. Resonant absorption of energy by the protons due to an external oscillating magnetic field will occur at the Larmor frequency for the particular nucleus.
The spin of the proton has two states. The net longitudinal magnetization in thermodynamical equilibrium is due to a tiny excess of protons in the lower energy state. This gives a net polarization parallel to the external field. Application of an RF pulse can tip sideways (with i.e. a so-called 90° pulse) or even reverse (with a so-called 180° pulse) this net polarization vector.
The recovery of longitudinal magnetization is called longitudinal or T1 relaxation and occurs exponentially with a time constant T1. The loss of phase coherence in the transverse plane is called transverse or T2 relaxation. T1 is thus associated with the enthalpy of the spin system (the number of nuclei with parallel versus anti-parallel spin) while T2 is associated with its entropy (the number of nuclei in phase).
When the radio frequency pulse is turned off, the transverse vector component produces an oscillating magnetic field which induces a small current in the receiver coil. This signal is called the free induction decay (FID). In an idealized nuclear magnetic resonance experiment, the FID decays approximately exponentially with a time constant T2, but in practical MRI small differences in the static magnetic field at different spatial locations ("inhomogeneities") cause the Larmor frequency to vary across the body creating destructive interference which shortens the FID. The time constant for the observed decay of the FID is called the T*
2 relaxation time, and is always shorter than T2. Also, when the radio frequency pulse is turned off, the longitudinal magnetization starts to recover exponentially with a time constant T1.
In MRI, the static magnetic field is caused to vary across the body (a field gradient), so that different spatial locations become associated with different precession frequencies. Usually these field gradients are pulsed, and it is the almost infinite variety of RF and gradient pulse sequences that gives MRI its versatility. Application of field gradient destroys the FID signal, but this can be recovered and measured by a refocusing gradient (to create a so-called "gradient echo"), or by a radio frequency pulse (to create a so-called "spin-echo"). The whole process can be repeated when some T1-relaxation has occurred and the thermal equilibrium of the spins has been more or less restored.
Typically in soft tissues T1 is around one second while T2 and T*
2 are a few tens of milliseconds, but these values vary widely between different tissues (and different external magnetic fields), giving MRI its tremendous soft tissue contrast.
Contrast agents work by altering (shortening) the relaxation parameters, especially T1.
Imaging
A number of schemes have been devised for combining field gradients and radio frequency excitation to create an image:
- 2D or 3D reconstruction from projections, much as in computed tomography.
- Building the image point-by-point or line-by-line.
- Gradients in the RF field rather than the static field.
Although each of these schemes is occasionally used in specialist applications, the majority of MR Images today are created either by the two-dimensional Fourier transform (2DFT) technique with slice selection, or by the three-dimensional Fourier transform (3DFT) technique. Another name for 2DFT is spin-warp. What follows here is a description of the 2DFT technique with slice selection.
The 3DFT technique is rather similar except that there is no slice selection and phase-encoding is performed in two separate directions.
Another scheme which is sometimes used, especially in brain scanning or where images are needed very rapidly, is called echo-planar imaging (EPI): In this case, each RF excitation is followed by a train of gradient echoes with different spatial encoding.
Image contrast and contrast enhancement
Image contrast is created by differences in the strength of the NMR signal recovered from different locations within the sample. This depends upon the relative density of excited nuclei (usually water protons), on differences in relaxation times (T1, T2, and T*
2) of those nuclei after the pulse sequence, and often on other parameters discussed under specialized MR scans. Contrast in most MR images is actually a mixture of all these effects, but careful design of the imaging pulse sequence allows one contrast mechanism to be emphasized while the others are minimized. The ability to choose different contrast mechanisms gives MRI tremendous flexibility. In the brain, T1-weighting causes the nerve connections of white matter to appear white, and the congregations of neurons of gray matter to appear gray, while cerebrospinal fluid (CSF) appears dark. The contrast of white matter, gray matter and cerebrospinal fluid is reversed using T2 or T*
2 imaging, whereas proton-density-weighted imaging provides little contrast in healthy subjects. Additionally, functional parameters such as cerebral blood flow (CBF), cerebral blood volume (CBV) or blood oxygenation can affect T1, T2 and T*
2 and so can be encoded with suitable pulse sequences.
In some situations it is not possible to generate enough image contrast to adequately show the anatomy or pathology of interest by adjusting the imaging parameters alone, in which case a contrast agent may be administered. This can be as simple as water, taken orally, for imaging the stomach and small bowel. However, most contrast agents used in MRI are selected for their specific magnetic properties. Most commonly, a paramagnetic contrast agent (usually a gadolinium compound[2][3]) is given. Gadolinium-enhanced tissues and fluids appear extremely bright on T1-weighted images. This provides high sensitivity for detection of vascular tissues (e.g., tumors) and permits assessment of brain perfusion (e.g., in stroke). There have been concerns raised recently regarding the toxicity of gadolinium-based contrast agents and their impact on persons with impaired kidney function. (See Safety/Contrast agents below.)
More recently, superparamagnetic contrast agents, e.g., iron oxide nanoparticles[4][5], have become available. These agents appear very dark on T
2-weighted images and may be used for liver imaging, as normal liver tissue retains the agent, but abnormal areas (e.g., scars, tumors) do not. They can also be taken orally, to improve visualization of the gastrointestinal tract, and to prevent water in the gastrointestinal tract from obscuring other organs (e.g., the pancreas). Diamagnetic agents such as barium sulfate have also been studied for potential use in the gastrointestinal tract, but are less frequently used.
k-space
In 1983 Ljunggren[6] and Twieg[7] independently introduced the k-space formalism, a technique that proved invaluable in unifying different MR imaging techniques. They showed that the demodulated MR signal S(t) generated by freely precessing nuclear spins in the presence of a linear magnetic field gradient G equals the Fourier transform of the effective spin density. Mathematically:
where:
In other words, as time progresses the signal traces out a trajectory in k-space with the velocity vector of the trajectory proportional to the vector of the applied magnetic field gradient. By the term effective spin density we mean the true spin density 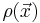 corrected for the effects of T1 preparation, T2 decay, dephasing due to field inhomogeneity, flow, diffusion, etc. and any other phenomena that affect that amount of transverse magnetization available to induce signal in the RF probe.
corrected for the effects of T1 preparation, T2 decay, dephasing due to field inhomogeneity, flow, diffusion, etc. and any other phenomena that affect that amount of transverse magnetization available to induce signal in the RF probe.
From the basic k-space formula, it follows immediately that we reconstruct an image 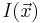 simply by taking the inverse Fourier transform of the sampled data, viz.
simply by taking the inverse Fourier transform of the sampled data, viz.
Using the k-space formalism, a number of seemingly complex ideas became simple. For example, it becomes very easy to understand the role of phase encoding (the so-called spin-warp method). In a standard spin echo or gradient echo scan, where the readout (or view) gradient is constant (e.g. G), a single line of k-space is scanned per RF excitation. When the phase encoding gradient is zero, the line scanned is the kx axis. When a non-zero phase-encoding pulse is added in between the RF excitation and the commencement of the readout gradient, this line moves up or down in k-space, i.e., we scan the line ky = constant.
The k-space formalism also makes it very easy to compare different scanning techniques. In single-shot EPI, all of k-space is scanned in a single shot, following either a sinusoidal or zig-zag trajectory. Since alternating lines of k-space are scanned in opposite directions, this must be taken into account in the reconstruction. Multi-shot EPI and fast spin echo techniques acquire only part of k-space per excitation. In each shot, a different interleaved segment is acquired, and the shots are repeated until k-space is sufficiently well-covered. Since the data at the center of k-space represent lower spatial frequencies than the data at the edges of k-space, the TE value for the center of k-space determines the image's T2 contrast.
The importance of the center of k-space in determining image contrast can be exploited in more advanced imaging techniques. One such technique is spiral acquisition—a rotating magnetic field gradient is applied, causing the trajectory in k-space to spiral out from the center to the edge. Due to T2 andT*
2 decay the signal is greatest at the start of the acquisition, hence acquiring the center of k-space first improves contrast to noise ratio (CNR) when compared to conventional zig-zag acquisitions, especially in the presence of rapid movement.
Since 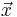 and
and 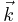 are conjugate variables (with respect to the Fourier transform) we can use the Nyquist theorem to show that the step in k-space determines the field of view of the image (maximum frequency that is correctly sampled) and the maximum value of k sampled determines the resolution, i.e.
are conjugate variables (with respect to the Fourier transform) we can use the Nyquist theorem to show that the step in k-space determines the field of view of the image (maximum frequency that is correctly sampled) and the maximum value of k sampled determines the resolution, i.e.
(These relationships apply to each axis independently.)
Example of a pulse sequence
In the timing diagram, the horizontal axis represents time. The vertical axis represents: (top row) amplitude of radio frequency pulses; (middle rows) amplitudes of the three orthogonal magnetic field gradient pulses; and (bottom row) receiver analog-to-digital converter (ADC). Radio frequencies are transmitted at the Larmor frequency of the nuclide to be imaged. For example, for 1H in a magnetic field of 1 T, a frequency of 42.5781 MHz would be employed. The three field gradients are labeled GX (typically corresponding to a patient's left-to-right direction and colored red in diagram), GY (typically corresponding to a patient's front-to-back direction and colored green in diagram), and GZ (typically corresponding to a patient's head-to-toe direction and colored blue in diagram). Where negative-going gradient pulses are shown, they represent reversal of the gradient direction, i.e., right-to-left, back-to-front or toe-to-head. For human scanning, gradient strengths of 1–100 mT/m are employed: Higher gradient strengths permit better resolution and faster imaging. The pulse sequence shown here would produce a transverse (axial) image.
The first part of the pulse sequence, SS, achieves 'slice selection'. A shaped pulse (shown here with a sinc modulation) causes a 90° nutation of longitudinal nuclear magnetization within a slab, or slice, creating transverse magnetization. The second part of the pulse sequence, PE, imparts a phase shift upon the slice-selected nuclear magnetization, varying with its location in the Y direction. The third part of the pulse sequence, another slice selection (of the same slice) uses another shaped pulse to cause a 180° rotation of transverse nuclear magnetization within the slice. This transverse magnetisation refocuses to form a spin echo at a time TE. During the spin echo, a frequency-encoding (FE) or readout gradient is applied, making the resonant frequency of the nuclear magnetization vary with its location in the X direction. The signal is sampled nFE times by the ADC during this period, as represented by the vertical lines. Typically nFE of between 128 and 512 samples are taken.
The longitudinal magnetisation is then allowed to recover somewhat and after a time TR the whole sequence is repeated nPE times, but with the phase-encoding gradient incremented (indicated by the horizontal hatching in the green gradient block). Typically nPE of between 128 and 512 repetitions are made.
The negative-going lobes in GX and GZ are imposed to ensure that, at time TE (the spin echo maximum), phase only encodes spatial location in the Y direction.
Typically TE is between 5 ms and 100 ms, while TR is between 100 ms and 2000 ms.
After the two-dimensional matrix (typical dimension between 128 × 128 and 512 × 512) has been acquired, producing the so-called k-space data, a two-dimensional Fourier transform is performed to provide the familiar MR image. Either the magnitude or phase of the Fourier transform can be taken, the former being far more common.
Scanner construction and operation
The major components of an MRI scanner are: the main magnet, which polarizes the sample, the shim coils for correcting inhomogeneities in the main magnetic field, the gradient system which is used to localize the MR signal and the RF system, which excites the sample and detects the resulting NMR signal. The whole system is controlled by one or more computers.
Magnet
The magnet is the largest and most expensive component of the scanner, and the remainder of the scanner is built around it. The strength of the magnet is measured in teslas (T). Clinical magnets generally have a field strength in the range 0.1–3.0 T, with research systems available up to 9.4 T for human use and 21 T for animal systems.[8]
Just as important as the strength of the main magnet is its precision. The straightness of the magnetic lines within the center (or, as it is technically known, the iso-center) of the magnet needs to be near-perfect. This is known as homogeneity. Fluctuations (inhomogeneities in the field strength) within the scan region should be less than three parts per million (3 ppm). Three types of magnets have been used:
- Permanent magnet: Conventional magnets made from ferromagnetic materials (e.g., steel alloys containing rare earth elements such as neodymium) can be used to provide the static magnetic field. A permanent magnet that is powerful enough to be used in an MRI will be extremely large and bulky; they can weigh over 100 tonnes. Permanent magnet MRIs are very inexpensive to maintain; this cannot be said of the other types of MRI magnets, but there are significant drawbacks to using permanent magnets. They are only capable of achieving weak field strengths compared to other MRI magnets (usually less than 0.4 T) and they are of limited precision and stability. Permanent magnets also present special safety issues; since their magnetic fields cannot be "turned off," ferromagnetic objects are virtually impossible to remove from them once they come into direct contact. Permanent magnets also require special care when they are being brought to their site of installation.
- Resistive electromagnet: A solenoid wound from copper wire is an alternative to a permanent magnet. An advantage is low initial cost, but field strength and stability are limited. The electromagnet requires considerable electrical energy during operation which can make it expensive to operate. This design is essentially obsolete.
- Superconducting electromagnet: When a niobium-titanium or niobium-tin alloy is cooled by liquid helium to 4 K (−269 °C, −452 °F) it becomes a superconductor, losing resistance to flow of electrical current. An electromagnet constructed with superconductors can have extremely high field strengths, with very high stability. The construction of such magnets is extremely costly, and the cryogenic helium is expensive and difficult to handle. However, despite their cost, helium cooled superconducting magnets are the most common type found in MRI scanners today.
Most superconducting magnets have their coils of superconductive wire immersed in liquid helium, inside a vessel called a cryostat. Despite thermal insulation, sometimes including a second cryostat containing liquid nitrogen, ambient heat causes the helium to slowly boil off. Such magnets, therefore, require regular topping-up with liquid helium. Generally a cryocooler, also known as a coldhead, is used to recondense some helium vapor back into the liquid helium bath. Several manufacturers now offer 'cryogenless' scanners, where instead of being immersed in liquid helium the magnet wire is cooled directly by a cryocooler.[9]
Magnets are available in a variety of shapes. However, permanent magnets are most frequently 'C' shaped, and superconducting magnets most frequently cylindrical. However, C-shaped superconducting magnets and box-shaped permanent magnets have also been used.
Magnetic field strength is an important factor in determining image quality. Higher magnetic fields increase signal-to-noise ratio, permitting higher resolution or faster scanning. However, higher field strengths require more costly magnets with higher maintenance costs, and have increased safety concerns. A field strength of 1.0–1.5 T is a good compromise between cost and performance for general medical use. However, for certain specialist uses (e.g., brain imaging) higher field strengths are desirable, with some hospitals now using 3.0 T scanners.
Shims
When the MR scanner is placed in the hospital or clinic, its main magnetic field is far from being homogeneous enough to be used for scanning. That is why before doing fine tuning of the field using a sample, the magnetic field of the magnet must be measured and shimmed.
After a sample is placed into the scanner, the main magnetic field is distorted by susceptibility boundaries within that sample, causing signal dropout (regions showing no signal) and spatial distortions in acquired images. For humans or animals the effect is particularly pronounced at air-tissue boundaries such as the sinuses (due to paramagnetic oxygen in air) making, for example, the frontal lobes of the brain difficult to image. To restore field homogeneity a set of shim coils is included in the scanner. These are resistive coils, usually at room temperature, capable of producing field corrections distributed as several orders of spherical harmonics.[10]
After placing the sample in the scanner, the B0 field is 'shimmed' by adjusting currents in the shim coils. Field homogeneity is measured by examining an FID signal in the absence of field gradients. The FID from a poorly shimmed sample will show a complex decay envelope, often with many humps. Shim currents are then adjusted to produce a large amplitude exponentially decaying FID, indicating a homogeneous B0 field. The process is usually automated.[11]
Gradients
Gradient coils are used to spatially encode the positions of protons by varying the magnetic field linearly across the imaging volume. The Larmor frequency will then vary as a function of position in the x, y and z-axes.
Gradient coils are usually resistive electromagnets powered by sophisticated amplifiers which permit rapid and precise adjustments to their field strength and direction. Typical gradient systems are capable of producing gradients from 20 mT/m to 100 mT/m (i.e., in a 1.5 T magnet, when a maximal z-axis gradient is applied, the field strength may be 1.45 T at one end of a 1 m long bore and 1.55 T at the other[12]). It is the magnetic gradients that determine the plane of imaging—because the orthogonal gradients can be combined freely, any plane can be selected for imaging.
Scan speed is dependent on performance of the gradient system. Stronger gradients allow for faster imaging, or for higher resolution; similarly, gradient systems capable of faster switching can also permit faster scanning. However, gradient performance is limited by safety concerns over nerve stimulation.
Some important characteristics of gradient amplifiers and gradient coils are slew rate and gradient strength. As mentioned earlier, a gradient coil will create an additional, linearly varying magnetic field that adds or subtracts from the main magnetic field. This additional magnetic field will have components in all 3 directions, viz. x, y and z; however, only the component along the magnetic field (usually called the z-axis, hence denoted Gz) is useful for imaging. Along any given axis, the gradient will add to the magnetic field on one side of the zero position and subtract from it on the other side. Since the additional field is a gradient, it has units of gauss per centimeter or millitesla per meter (mT/m). High performance gradient coils used in MRI are typically capable of producing a gradient magnetic field of approximate 30 mT/m or higher for a 1.5 T MRI. The slew rate of a gradient system is a measure of how quickly the gradients can be ramped on or off. Typical higher performance gradients have a slew rate of up to 100–200 T·m−1·s−1. The slew rate depends both on the gradient coil (it takes more time to ramp up or down a large coil than a small coil) and on the performance of the gradient amplifier (it takes a lot of voltage to overcome the inductance of the coil) and has significant influence on image quality.
Radio frequency system
The radio frequency (RF) transmission system consists of an RF synthesizer, power amplifier and transmitting coil. That coil is usually built into the body of the scanner. The power of the transmitter is variable, but high-end whole-body scanners may have a peak output power of up to 35 kW,[13] and be capable of sustaining average power of 1 kW. The receiver consists of the coil, pre-amplifier and signal processing system. While it is possible to scan using the integrated coil for RF transmission and MR signal reception, if a small region is being imaged, then better image quality (i.e. higher signal-to-noise ratio) is obtained by using a close-fitting smaller coil. A variety of coils are available which fit closely around parts of the body such as the head, knee, wrist, breast, or internally, e.g. the rectum.
A recent development in MRI technology has been the development of sophisticated multi-element phased array[14] coils which are capable of acquiring multiple channels of data in parallel. This 'parallel imaging' technique uses unique acquisition schemes that allow for accelerated imaging, by replacing some of the spatial coding originating from the magnetic gradients with the spatial sensitivity of the different coil elements. However, the increased acceleration also reduces the signal-to-noise ratio and can create residual artifacts in the image reconstruction. Two frequently used parallel acquisition and reconstruction schemes are known as SENSE[15] and GRAPPA.[16] A detailed review of parallel imaging techniques can be found here:[17]
References
- ^ Callaghan P (1994). Principles of Nuclear Magnetic Resonance Microscopy. Oxford University Press. ISBN 0198539975.
- ^ Weinmann HJ, Brasch RC, Press WR, Wesbey GE (1984). "Characteristics of gadolinium-DTPA complex: A potential NMR contrast agent". American Journal of Roentgenology 142 (3): 619–624. PMID 6607655. http://www.ajronline.org/cgi/pmidlookup?view=long&pmid=6607655.
- ^ Laniado M, Weinmann HJ, Schörner W, Felix R, Speck U (1984). "First use of GdDTPA/dimeglumine in man". Physiological Chemistry & Physics & Medical NMR 16 (2): 157–165. PMID 6505042.
- ^ Widder DJ, Greif WL, Widder KJ, Edelman RR, Brady TJ (1987). "Magnetite albumin microspheres: A new MR contrast material". American Journal of Roentgenology 148 (2): 399–404. PMID 3492120. http://www.ajronline.org/cgi/pmidlookup?view=long&pmid=3492120.
- ^ Weissleder R, Elizondo G, Wittenberg J, Rabito CA, Bengele HH, Josephson L (1990). "Ultrasmall superparamagnetic iron oxide: Characterization of a new class of contrast agents for MR imaging". Radiology 175 (2): 489–493. PMID 2326474. http://radiology.rsnajnls.org/cgi/pmidlookup?view=long&pmid=2326474.
- ^ Ljunggren S (1983). "A simple graphical representation of Fourier-based imaging methods". Journal of Magnetic Resonance 54 (2): 338–343. doi:10.1016/0022-2364(83)90060-4.
- ^ Twieg D (1983). "The k-trajectory formulation of the NMR imaging process with applications in analysis and synthesis of imaging methods". Medical Physics 10 (5): 610–621. doi:10.1118/1.595331. PMID 6646065.
- ^ "In vivo MR Imaging at 21.1 T". http://www.magnet.fsu.edu/mediacenter/factsheets/documents/invivomri-maglabreports-2007-v14-i4.pdf.
- ^ Obasih, K. M.; Mruzek, M. T. (1996). "Thermal design and analysis of a cryogenless superconducting magnet for interventional MRI therapy". In Timmerhaus, K. D.. Proceedings of the 1995 cryogenic engineering conference. New York: Plenum Press. pp. 305–312. ISBN 0306453002.
- ^ Chen CN, Hoult DH (1989). Biomedical Magnetic Resonance Technology. Medical Sciences. Taylor & Francis. ISBN 978-0852741184.
- ^ Gruetter R (1992). "Automatic, localized in Vivo adjustment of all first-and second-order shim coils.". Magnetic Resonance in Medicine 29 (6): 804–811. doi:10.1002/mrm.1910290613. PMID 8350724.
- ^ This unrealistically assumes that the gradient is linear out to the end of the magnet bore. While this assumption is fine for pedagogical purposes, in most commercial MRI systems the gradient droops significantly after a much smaller distance; indeed, the decrease in the gradient field is the main delimiter of the useful field of view of a modern commercial MRI system.
- ^ Oppelt A (2006). Imaging Systems for Medical Diagnostics: Fundamentals, Technical Solutions and Applications for Systems Applying Ionizing Radiation, Nuclear Magnetic Resonance and Ultrasound. Wiley-VCH. p. 566. ISBN 978-3895782268.
- ^ Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM (1990). "The NMR phased array". Magnetic Resonance in Medicine 16 (2): 192–225. doi:10.1002/mrm.1910160203. PMID 2266841.
- ^ Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P (1999). "SENSE: Sensitivity encoding for fast MRI". Magnetic Resonance in Medicine 42 (5): 952–962. doi:10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S. PMID 10542355.
- ^ Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A (2002). "Generalized autocalibrating partially parallel acquisitions (GRAPPA)". Magnetic Resonance in Medicine 47 (6): 1202–1210. doi:10.1002/mrm.10171. PMID 12111967.
- ^ Blaimer M, Breuer F, Mueller M, Heidemann RM, Griswold MA, Jakob PM (2004). "SMASH, SENSE, PILS, GRAPPA: How to Choose the Optimal Method". Topics in Magnetic Resonance Imaging 15 (4): 223–236. doi:10.1097/01.rmr.0000136558.09801.dd. http://cfmriweb.ucsd.edu/ttliu/be280a_05/blaimer05.pdf.